

|
EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software |
|
EIDORS
(mirror) Main Documentation Tutorials − Image Reconst − Data Structures − Applications − FEM Modelling − GREIT − Old tutorials − Workshop Download Contrib Data GREIT Browse Docs Browse SVN News Mailing list (archive) FAQ Developer
|
GREIT Reconstruction in 3DCode for Reconstruction using GREIT in 3D was recently added. If you have EIDORS v3.9, you will need the following two files: For 3D distributions, using GREIT 3D is much better, even if you only want a single slice. See, for exampleGrychtol et al, Focusing EIT reconstructions using two electrode planes p. 17 Conf. EIT 2017, Dartmouth, NH, USA, June 21−24, 2017.This code is also very slow to calculate. The actual reconstruction is fast. There are numerous improvements possible, and they're being worked on. Model of a tank with an object moving vertically
%STEP 1: Simple model with vertical targets
posns= linspace(0.5,3.5,13);
str=''; for i=1:length(posns);
extra{i} = sprintf('ball%03d',round(posns(i)*100));
str = [str,sprintf('solid %s=sphere(0.5,0,%f;0.1); ', extra{i}, posns(i))];
end
extra{i+1} = str;
fmdl= ng_mk_cyl_models([4,1,.2],[16,1.5,2.5],[0.05],extra);
fmdl = mdl_normalize(fmdl, 0);
[~,fmdl] = elec_rearrange([16,2],'square', fmdl);
img= mk_image(fmdl,1);
img.elem_data(vertcat(fmdl.mat_idx{2:end}))= 2;
opt.viewpoint = struct('az',0,'el',10);
clf;show_fem_enhanced(img,opt);
print_convert GREIT3D_tank01a.jpg
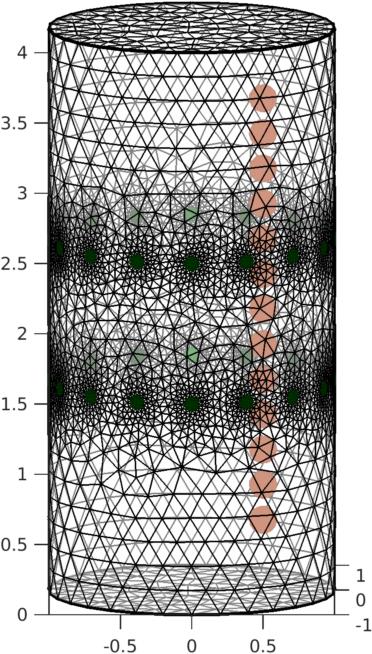
Figure: Simulation cylindrical tank with objects in a vertical plane Simulate data from tank
% STEP 2: Simulate data
[fmdl.stimulation,fmdl.meas_select] = mk_stim_patterns(32,1,[0,5],[0,5],{},1);
img= mk_image(fmdl,1);
vh = fwd_solve(img);
for i=1:length(posns)-4;
img= mk_image(fmdl,1);
img.elem_data(fmdl.mat_idx{i+1}) = 2;
vi{i} = fwd_solve(img);
end;
Create reconstruction modelA new model to ensure we don't commit an inverse crime. Note that we use the "square" electrode configuration with a "skip 4" stimulation and measurement pattern.
% STEP 3: Reconstruction model
fmdl= ng_mk_cyl_models([4,1,.5],[16,1.5,2.5],[0.05]);
[fmdl.stimulation,fmdl.meas_select] = mk_stim_patterns(32,1,[0,5],[0,5],{},1);
fmdl = mdl_normalize(fmdl, 0);
[~,fmdl] = elec_rearrange([16,2],'square', fmdl);
GREIT 2DHere we build a 2D GREIT reconstruction, using training targets only in the centre plane.% STEP 4: Reconstruction using GREIT 2D opt.imgsz = [32 32]; opt.square_pixels = true; opt.noise_figure = 0.5; img = mk_image(fmdl,1); imdl2 = mk_GREIT_model(img, 0.25, [], opt);And reconstruct the first 9 targets, from the bottom
img = inv_solve(imdl2,vh,[vi{:}]);
img.show_slices.img_cols= 9;
show_slices(img);
print_convert GREIT3D_tank05a.jpg

Figure: Reconstruction of 9 targets moving from the bottom of the tank using a 2D GREIT version GREIT 3DHere we build a 3D GREIT reconstruction, using training targets only in all planes% STEP 4: Reconstruction using GREIT 3D vopt.imgsz = [32 32]; vopt.zvec = linspace( 0.75,3.25,6); vopt.save_memory = 1; opt.noise_figure = 2.0; [imdl,opt.distr] = GREIT3D_distribution(fmdl, vopt); imdl3= mk_GREIT_model(imdl, 0.20, [], opt);And reconstruct the first 9 targets, from the bottom
img = inv_solve(imdl3,vh,[vi{:}]);
img.show_slices.img_cols= 9;
levels = [inf,inf,1.5;
inf,inf,2.0];
show_slices(img,levels);
print_convert GREIT3D_tank07a.jpg
img.elem_data = img.elem_data(:,4); % choose 4th image
show_fem(img);
print_convert GREIT3D_tank07b.jpg
show_3d_slices(img,[1.5,2],0,0); view(-16,18);
print_convert GREIT3D_tank07c.jpg
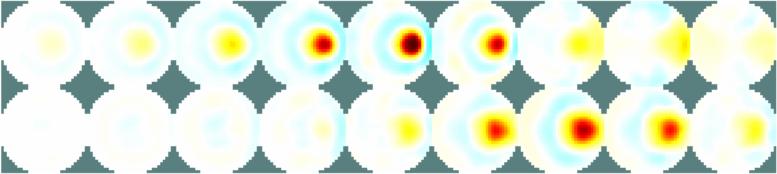
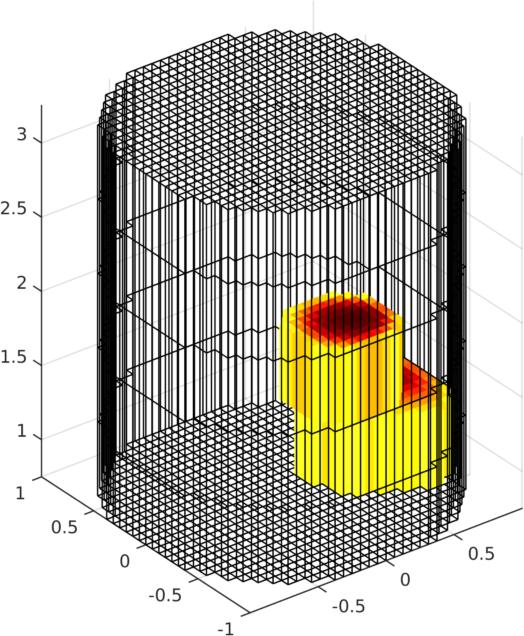
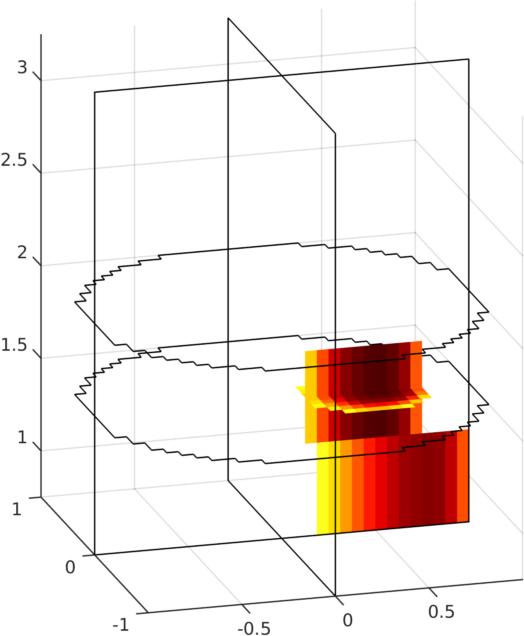
Figure: Left Reconstruction of 9 targets moving from the bottom of the tank using a 3D GREIT version, in two planes. The 4th image is then shown as a volume (Centre) or through cut-planes (Right) GREIT 3D − 2D slicesIn many cases, what is wanted are reconstructions to a slices of the volume, but using the GREIT 3D approach. This is what the solve_RM_2Dslice functions does.imdl3a= select_RM_slice(imdl3,1.5);The single-plane reconstruction matrix is then attached to imdl3a.solve_use_matrix.RM.
img = inv_solve(imdl3a,vh,[vi{:}]);
img.show_slices.img_cols= 9;
show_slices(img);
print_convert GREIT3D_tank09a.jpg

Figure: Reconstruction of 9 targets moving from the bottom of the tank using a slice at z=1.5 of the 3D GREIT version Last Modified: $Date: 2018-03-28 15:01:38 -0400 (Wed, 28 Mar 2018) $ by $Author: aadler $ |