EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

GREIT Reconstruction Examples

Simulate 3D object

% Simulate obj $Id: GREIT_examples01.m 2775 2011-07-14 17:21:55Z aadler $

fmdl = ng_mk_cyl_models([2,1,0.1],[16,1],[0.05]); 
fmdl.stimulation = mk_stim_patterns(16,1,[0,1],[0,1],{},1);

% Homogeneous object
imgh= mk_image( fmdl, 1 );
% Fwd Simulation
vh = fwd_solve( imgh);

% Target Object
select_fcn = inline('(x-0.2).^2 + (y-0.5).^2 + (z-1).^2<0.1^2','x','y','z');
memb_frac = elem_select( imgh.fwd_model, select_fcn);
imgt= mk_image( fmdl, 1 + memb_frac );
% Fwd Simulation
vt = fwd_solve( imgt);

% Add SNR 2.0 noise
vn = add_noise(4, vt, vh);

clf; show_fem(imgt);
print_convert GREIT_examples01a.png

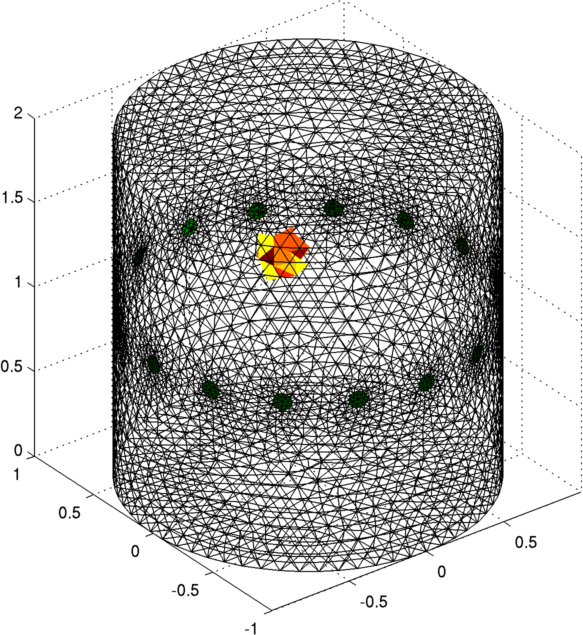
Figure: Simulation Mesh and object

Reconstruct (no noise)

% Simulate obj $Id: GREIT_examples02.m 4839 2015-03-30 07:44:50Z aadler $

% GREIT v1
i_gr = mk_common_gridmdl('GREITc1');

show_fem( inv_solve( i_gr, vh, vt) ); axis equal;
print_convert 'GREIT_examples02a.png' '-density 50'; 

% current GREIT recommendation
opt.noise_figure = 0.5;
opt.distr = 0; % best for cylinders
i_grc = mk_GREIT_model(fmdl,.2,[],opt);
show_fem( inv_solve( i_grc, vh, vt) ); axis equal;
print_convert 'GREIT_examples02b.png' '-density 50'; 

% Sheffield Backprojection
i_bp = mk_common_gridmdl('backproj');

show_fem( inv_solve( i_bp, vh, vt) ); axis equal;
print_convert 'GREIT_examples02c.png' '-density 50';

% 2D Gauss Newton Inverse
i_gn = mk_common_model('d2c2',16);
i_gn.hyperparameter.value = 0.1;
i_gn.fwd_model = mdl_normalize(i_gn.fwd_model, 1);
% i_gn.RtR_prior = @prior_gaussian_HPF;

show_fem( inv_solve( i_gn, vh, vt) ); axis equal;
print_convert 'GREIT_examples02d.png' '-density 50';

% Test the Noise Figure of the GN inverse => 0.5
% i_gn.hyperparameter.tgt_data.meas_t1 = vh;
% i_gn.hyperparameter.tgt_data.meas_t2 = vt;
% calc_noise_figure(i_gn)

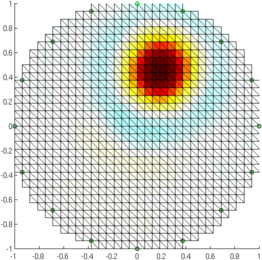
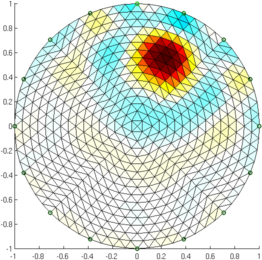
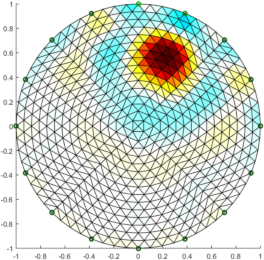
Figure: Reconstruction (no noise) with (from left to right) GREIT v1, current GREIT recommendations, Sheffield Backprojection, Gauss Newton Inverse

Reconstruct (added noise)

% Simulate obj $Id: GREIT_examples03.m 4823 2015-03-29 15:17:16Z bgrychtol-ipa $

% GREIT v1
show_fem( inv_solve( i_gr, vh, vn) ); axis equal;
print_convert 'GREIT_examples03a.png' '-density 50';

% current GREIT
show_fem( inv_solve( i_grc, vh, vn) ); axis equal;
print_convert 'GREIT_examples03b.png' '-density 50';

% Sheffield Backprojection
show_fem( inv_solve( i_bp, vh, vn) ); axis equal;
print_convert 'GREIT_examples03c.png' '-density 50';

% 2D Gauss Newton Inverse
show_fem( inv_solve( i_gn, vh, vn) ); axis equal;
print_convert 'GREIT_examples03d.png' '-density 50';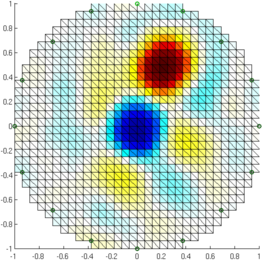

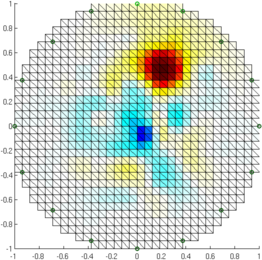
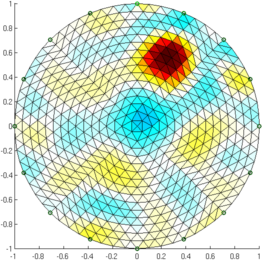
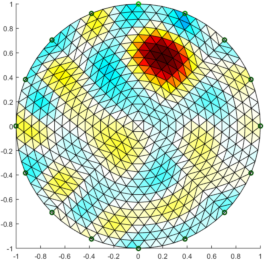
Figure: Reconstruction (SNR=0.5 noise) with (from left to right) GREIT v1, Current GREIT, Sheffield Backprojection, Gauss Newton Inverse