EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

GREIT Test Parameters

Figure: GREIT test parameters: Amplitude (AR), Position Error (PE), Resolution (RES), Shape Deformation (SD), Ringing (RNG)

Simulate 3D object

% Simulate obj $Id: GREIT_test_params01.m 2167 2010-04-04 21:39:48Z aadler $

fmdl = ng_mk_cyl_models([2,1,0.08],[16,1],[0.05]); 
fmdl.stimulation = mk_stim_patterns(16,1,[0,1],[0,1],{},1);
imgs= mk_image( fmdl, 1);

show_fem(imgs);
print_convert('GREIT_test_params01a.png','-density 60');

view(0,0)
xlim([-.4,.4])
zlim(1+[-.4,.4])
print_convert('GREIT_test_params01b.png','-density 60');

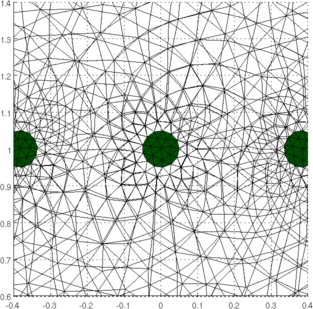
Figure: Simulation Mesh (right) and close-up of the electrodes (left)

Simulate Sequence of Targets

% Simulate obj $Id: GREIT_test_params02.m 4823 2015-03-29 15:17:16Z bgrychtol-ipa $

% Specify positions to simulate (only x-axis here)
r =  linspace(0,0.9,100);
xyzr = [r; zeros(1,100); ones(1,100);
     0.05*ones(1,100)];

[vh,vi] = simulate_movement(imgs, xyzr);

% Show GREIT images
opt.noise_figure = 0.5;
i_gr = mk_GREIT_model(fmdl,0.2,[],opt);
imgr = inv_solve(i_gr, vh, vi(:,1:5:100));
imgr.show_slices.img_cols = 5;
show_slices(imgr);

print_convert('GREIT_test_params02a.png','-density 60');

Figure: Illustration of the object locations in the simulation

Calculate the parameters

% GREIT params eval $Id: GREIT_test_params03.m 2240 2010-07-04 14:41:32Z aadler $

% Reconstruct GREIT Images
imdl_gr = mk_common_gridmdl('GREITc1');
imgc{1} = inv_solve(imdl_gr, vh, vi);

% Reconstruct backprojection Images
imdl_bp = mk_common_gridmdl('backproj');
imgc{2} = inv_solve(imdl_bp, vh, vi);

fname_base = 'GREIT_test_params04';

% GREIT params eval $Id: GREIT_test_params04.m 6504 2022-12-30 14:49:43Z aadler $

for i= 1:length(imgc);
   imgr = imgc{i};
   imgr.calc_colours.npoints = 32;
   params = eval_GREIT_fig_merit(imgr, xyzr);

   fname = sprintf('%s%c', fname_base, i+'a'-1);

   plot(r, params(1,:)); axis([0,0.9,0,2.0]);  ylabel('AR');
   print_convert([fname,'_ar.png'],  '-density 60','-p10x4');

   plot(r, params(2,:)); axis([0,0.9,-0.15,0.15]);  ylabel('PE');
   print_convert([fname,'_pe.png'],  '-density 60','-p10x4');

   plot(r, params(3,:)); axis([0,0.9,0,0.4]);  ylabel('RES');
   print_convert([fname,'_res.png'],  '-density 60','-p10x4');

   plot(r, params(4,:)); axis([0,0.9,0,0.3]);  ylabel('SD');
   print_convert([fname,'_sd.png'],  '-density 60','-p10x4');

   plot(r, params(5,:)); axis([0,0.9,0,0.6]);  ylabel('RNG');
   print_convert([fname,'_rng.png'],  '-density 60','-p10x4');
end

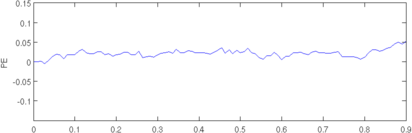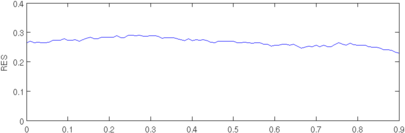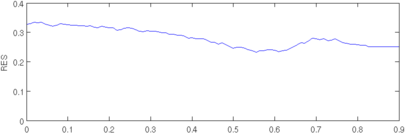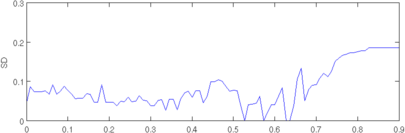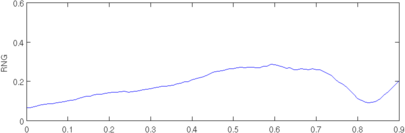Figure: Evaluation of GREIT (right), and Sheffield Backprojection (left) GREIT parameters AR, PE, RES, SD, and RNG as a function of point radial position

Comment

• The object is just in one x position in the plane. It should be rotated to all x,y positions.
• The various parameters are defined for a set of test positions for a given distance above and below the electrode plane, yet here we just test on the electrode plane.

Simulate Sequence of Targets above the plane (×25%)

% Simulate obj $Id: GREIT_test_params05.m 2167 2010-04-04 21:39:48Z aadler $

% Simulate positions that are 0.25 above the plane
r =  linspace(0,0.9,100);
xyzr = [r;
        zeros(1,100);
     1.25*ones(1,100);
     0.05*ones(1,100)];

[vh,vi] = simulate_movement(imgs, xyzr);

% Show GREIT images
i_gr = mk_common_gridmdl('GREITc1');
imgr = inv_solve(i_gr, vh, vi(:,1:5:100));
imgr.show_slices.img_cols = 5;
show_slices(imgr);

print_convert('GREIT_test_params05a.png','-density 60');

Figure: Illustration of the object locations in the simulation

Calculate the parameters

% GREIT params eval $Id: GREIT_test_params06.m 2240 2010-07-04 14:41:32Z aadler $

% Reconstruct GREIT Images
imdl_gr = mk_common_gridmdl('GREITc1');
imgc{1} = inv_solve(imdl_gr, vh, vi);

% Reconstruct backprojection Images
imdl_bp = mk_common_gridmdl('backproj');
imgc{2} = inv_solve(imdl_bp, vh, vi);

fname_base = 'GREIT_test_params06';

% GREIT params eval $Id: GREIT_test_params04.m 6504 2022-12-30 14:49:43Z aadler $

for i= 1:length(imgc);
   imgr = imgc{i};
   imgr.calc_colours.npoints = 32;
   params = eval_GREIT_fig_merit(imgr, xyzr);

   fname = sprintf('%s%c', fname_base, i+'a'-1);

   plot(r, params(1,:)); axis([0,0.9,0,2.0]);  ylabel('AR');
   print_convert([fname,'_ar.png'],  '-density 60','-p10x4');

   plot(r, params(2,:)); axis([0,0.9,-0.15,0.15]);  ylabel('PE');
   print_convert([fname,'_pe.png'],  '-density 60','-p10x4');

   plot(r, params(3,:)); axis([0,0.9,0,0.4]);  ylabel('RES');
   print_convert([fname,'_res.png'],  '-density 60','-p10x4');

   plot(r, params(4,:)); axis([0,0.9,0,0.3]);  ylabel('SD');
   print_convert([fname,'_sd.png'],  '-density 60','-p10x4');

   plot(r, params(5,:)); axis([0,0.9,0,0.6]);  ylabel('RNG');
   print_convert([fname,'_rng.png'],  '-density 60','-p10x4');
end

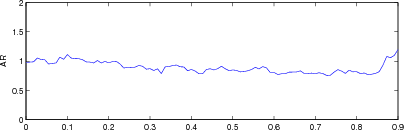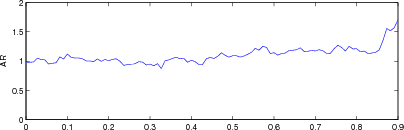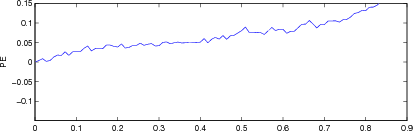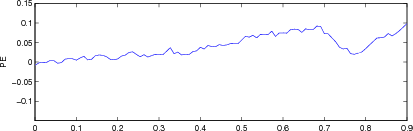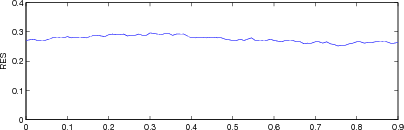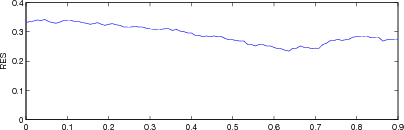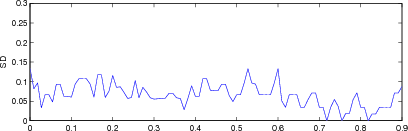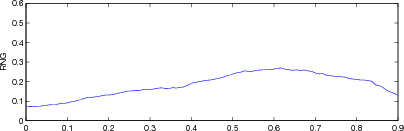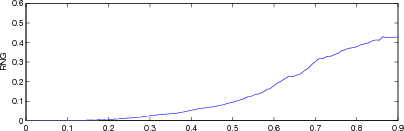Figure: Evaluation for off plane object (25%) of GREIT (left), and Sheffield Backprojection (right) GREIT parameters AR, PE, RES, SD, and RNG as a function of point radial position