EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

GREIT Reconstruction For different Model Geometries

Simulation model

% $Id: mk_GREIT_mat_ellip01.m 2799 2011-07-14 23:41:48Z bgrychtol $
n_elecs = 16;
stim =  mk_stim_patterns(n_elecs,1,[0,1],[0,1],{'no_meas_current'}, 1);

extra={'lungs','solid lungs = sphere(0.9,0.1,1;0.6) or sphere(-0.9,0.1,1;0.6);'};
[fmdl,midx] = ng_mk_ellip_models([2, 2,1.4,0.2] ,[n_elecs,1],[0.1], extra);
fmdl.stimulation =  stim;

img = mk_image(fmdl,1); % Homogeneous background
vh = fwd_solve(img);
img.elem_data(midx{2}) = 0.5; % Lung regions
vi = fwd_solve(img);

show_fem(img); view(0,70);
print_convert mk_GREIT_mat_ellip01a.png '-density 75'

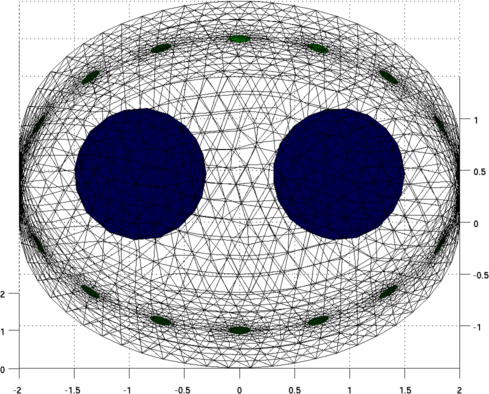
Figure: Simulation of data on an elliptical model with lung shaped contrasting regions

Calculate GREIT reconstruction matrices for various model shapes

% $Id: mk_GREIT_mat_ellip02.m 3350 2012-07-01 21:35:17Z bgrychtol $
opt.imgsz = [32 32];
opt.distr = 3; % non-random, uniform
opt.Nsim = 1000;
opt.target_size = 0.05; % Target size (frac of medium)
opt.noise_figure = 0.5; % Recommended NF=0.5;

k=1; for el = linspace(1,2.4,4);
   fmdl = ng_mk_ellip_models([2, 2,el,0.2] ,[n_elecs,1],[0.1]);
   fmdl.stimulation =  stim;
   fmdl = mdl_normalize(fmdl, 0);
   img = mk_image(fmdl,1);

   imdl(k) = mk_GREIT_model(img, 0.25, [], opt);

   subplot(1,4,k); show_fem(fmdl); view(0,70);
   k=k+1;
end

print_convert mk_GREIT_mat_ellip02.png '-density 180'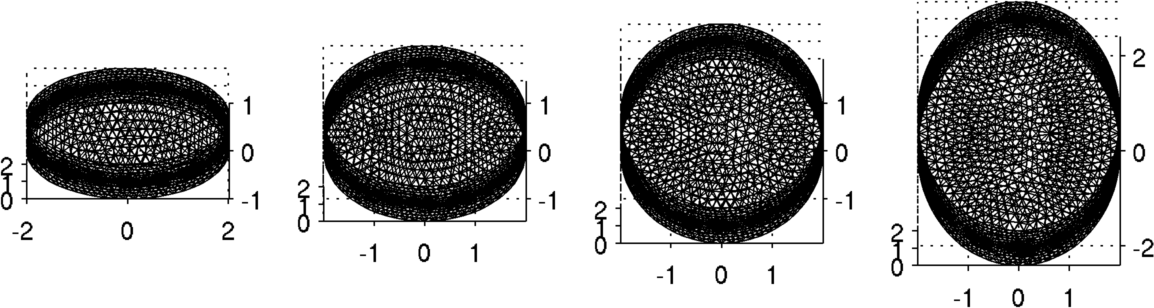

Figure: Four different elliptic reconstruction models with different elliptical parameters densities. The second from the left fits closest with the simulation data.

Reconstruct Images on each model

% $Id: mk_GREIT_mat_ellip03.m 2480 2011-03-03 20:43:07Z aadler $

for k=1:4
   rimg = inv_solve(imdl(k),vh,vi); %Reconstruct

   subplot(1,4,k)
   show_fem(rimg); axis square;
end

print_convert mk_GREIT_matrix03.png '-density 180'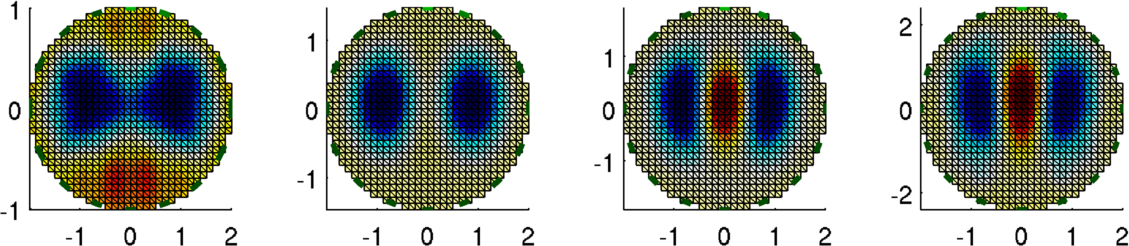

Figure: Four different elliptic reconstruction models with different densities.