EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

Dual Models to reconstruct a slice of a volume

To simulate this, we simulate a ball moving in a helical path on a fine netgen model (available here)

% Simulate Moving Ball - Helix $Id: centre_slice01.m 1535 2008-07-26 15:36:27Z aadler $

% get ng_mdl_16x2_vfine from data_contrib section of web page
n_sims= 20;
load ng_mdl_16x2_vfine.mat; fmdl= ng_mdl_16x2_vfine;
[vh,vi,xyzr_pt]= simulate_3d_movement( n_sims, fmdl);

show_fem(fmdl)
crop_model(gca, inline('x-z<-15','x','y','z'))
view(-23,14)

hold on
[xs,ys,zs]=sphere(10);
for i=1:n_sims
   xp=xyzr_pt(1,i); yp=xyzr_pt(2,i);
   zp=xyzr_pt(3,i); rp=xyzr_pt(4,i);
   hh=surf(rp*xs+xp, rp*ys+yp, rp*zs+zp);
   set(hh,'EdgeColor',[.4,0,.4],'FaceColor',[.2,0,.2]);
end
hold off

print -r100 -dpng centre_slice01a.png;

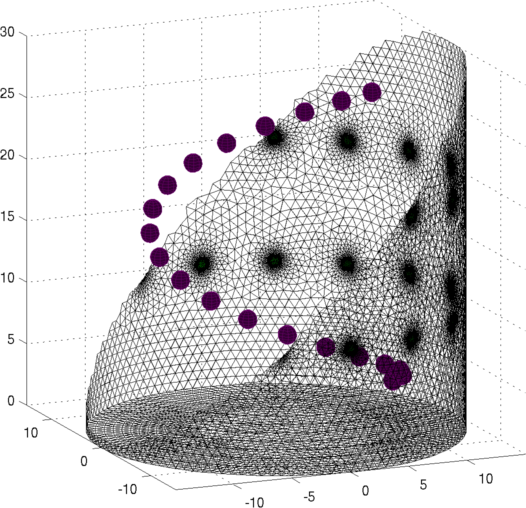
Figure: Netgen model of a 2×16 electrode tank. The positions of the simulated conductive target moving in a helical path are shown in purple.

Create reconstruction model

% 2D solver $Id: centre_slice02.m 1535 2008-07-26 15:36:27Z aadler $

% Create and show inverse solver
imdl = mk_common_model('b3cr',[16,2]);

load ng_mdl_16x2_coarse; f_mdl = ng_mdl_16x2_coarse;

imdl.fwd_model = f_mdl;

% Create coarse model
imdl2d= mk_common_model('b2c2',16);
c_mdl= imdl2d.fwd_model;

% Show fine model
show_fem(f_mdl);
crop_model(gca, inline('x-z<-15','x','y','z'))
view(-23,10)

scl= 15; % scale difference between c_mdl and f_mdl
c_els= c_mdl.elems;
c_ndsx= c_mdl.nodes(:,1)*scl;
c_ndsy= c_mdl.nodes(:,2)*scl;
c_ndsz= 0*c_ndsx; 

layersep= .3;
layerhig= .1;
hold on
% Lower resonstruction layer
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1-layersep)*scl);
set(hh, 'EdgeColor', [1,0,0]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1-layersep-layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1-layersep+layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);

% Upper resonstruction layer
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1+layersep)*scl);
set(hh, 'EdgeColor', [0,0,1]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1+layersep-layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(1+layersep+layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);

for i=1:n_sims
   xp=xyzr_pt(1,i); yp=xyzr_pt(2,i);
   zp=xyzr_pt(3,i); rp=xyzr_pt(4,i);
   hh=surf(rp*xs+xp, rp*ys+yp, rp*zs+zp);
   set(hh,'EdgeColor',[.4,0,.4]);
end

hold off;

print -r100 -dpng centre_slice02a.png;

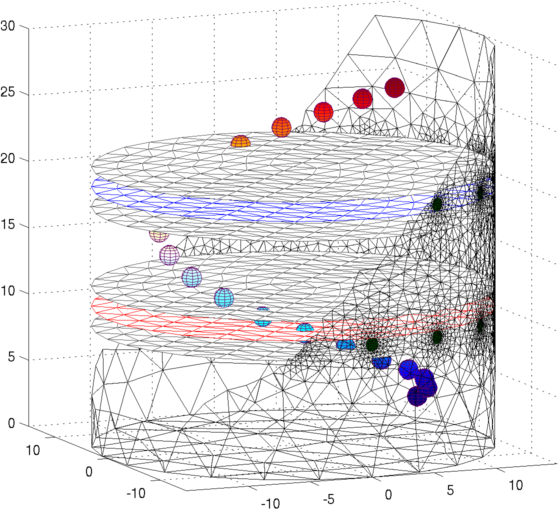
Figure: Netgen model of a 2×16 electrode tank. The positions of the simulated conductive target moving in a helical path are shown in purple. The 3D fine model is shown (cropped). The upper (blue) and lower (red) layers corresponding to the geometry of the coarse model are shown. The z direction limits of the coarse model are shown in grey.

Image reconstructions

% 2D solver $Id: centre_slice03.m 1535 2008-07-26 15:36:27Z aadler $


% Set coarse as reconstruction model
imdl.rec_model= c_mdl;
c_mdl.mk_coarse_fine_mapping.f2c_offset = [0,0,scl];
c_mdl.mk_coarse_fine_mapping.f2c_project = (1/scl)*speye(3);
c_mdl.mk_coarse_fine_mapping.z_depth = inf;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;
imdl.RtR_prior = @gaussian_HPF_prior;
imdl.solve = @aa_inv_solve;
imdl.hyperparameter.value= 0.01;

imgc= inv_solve(imdl, vh, vi);

subplot(131)
show_slices(imgc);

% 2D solver $Id: centre_slice04.m 1535 2008-07-26 15:36:27Z aadler $

imdl.hyperparameter.value= 0.003;

c_mdl.mk_coarse_fine_mapping.f2c_offset = [0,0,(1-.3)*scl];
c_mdl.mk_coarse_fine_mapping.z_depth = 0.1;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;
imgc0= inv_solve(imdl, vh, vi);
% Show image of reconstruction in upper planes
subplot(132)
show_slices(imgc0);

c_mdl.mk_coarse_fine_mapping.f2c_offset = [0,0,(1+.3)*scl];
c_mdl.mk_coarse_fine_mapping.z_depth = 0.1;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;
imgc1= inv_solve(imdl, vh, vi);

% Show image of reconstruction in lower planes
subplot(133)
show_slices(imgc1);

print -r150 -dpng centre_slice04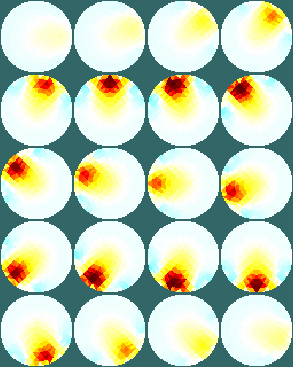a.png;

Figure: Reconstructed images of a target moving in a helical pattern using difference coarse models Left coarse model with z_depth=∞ Centrecoarse model with z_depth=0.1×scale at upper position Right coarse model with z_depth=0.1×scale at lower positions

Simpler reconstruction model

% 2D solver $Id: centre_slice05.m 1535 2008-07-26 15:36:27Z aadler $

% Create and show inverse solver
imdl = mk_common_model('b3cr',[16,2]);
f_mdl= imdl.fwd_model;

% Create coarse model
imdl2d= mk_common_model('b2c2',16);
c_mdl= imdl2d.fwd_model;

% Show fine model
show_fem(f_mdl);
crop_model(gca, inline('x-z<-.5','x','y','z'))
view(-23,10)

scl= 1; % scale difference between c_mdl and f_mdl
c_els= c_mdl.elems;
c_ndsx= c_mdl.nodes(:,1)*scl;
c_ndsy= c_mdl.nodes(:,2)*scl;
c_ndsz= 0*c_ndsx; 

layersep= .3;
layerhig= .1;
hold on
% Lower resonstruction layer
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(-layersep)*scl);
set(hh, 'EdgeColor', [1,0,0]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(-layersep-layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(-layersep+layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);

% Upper resonstruction layer
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(+layersep)*scl);
set(hh, 'EdgeColor', [0,0,1]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(+layersep-layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);
hh= trimesh(c_els, c_ndsx, c_ndsy, c_ndsz+(+layersep+layerhig)*scl);
set(hh, 'EdgeColor', [.3,.3,.3]);

[xs,ys,zs]=sphere(10);
for i=1:size(xyzr_pt,2)
   xp=xyzr_pt(1,i)/15;   yp=xyzr_pt(2,i)/15;
   zp=xyzr_pt(3,i)/15-1; rp=xyzr_pt(4,i)/15;
   hh=surf(rp*xs+xp, rp*ys+yp, rp*zs+zp);
   set(hh,'EdgeColor',[.4,0,.4]);
end

hold off;

print -r100 -dpng centre_slice05a.png;

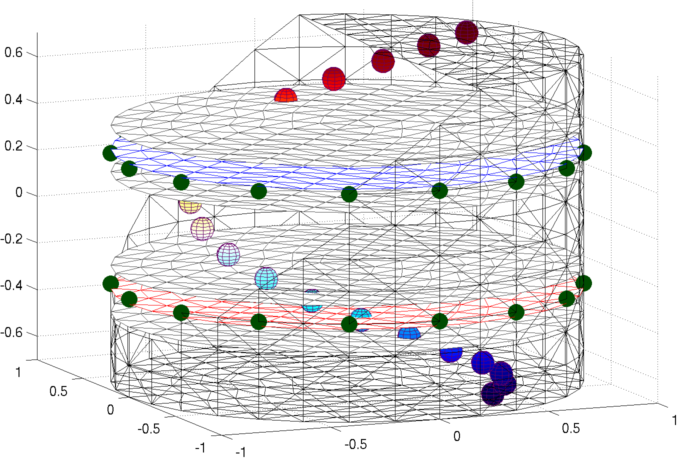
Figure: Simple extruded model of a 2×16 electrode tank. The positions of the simulated conductive target moving in a helical path are shown in purple. The 3D fine model is shown (cropped). The upper (blue) and lower (red) layers corresponding to the geometry of the coarse model are shown. The z direction limits of the coarse model are shown in grey.

Image reconstructions

% 2D solver $Id: centre_slice06.m 1535 2008-07-26 15:36:27Z aadler $


% Set coarse as reconstruction model
imdl.rec_model= c_mdl;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;
imdl.RtR_prior = @gaussian_HPF_prior;
imdl.solve = @aa_inv_solve;
imdl.hyperparameter.value= 0.03;

imgc= inv_solve(imdl, vh, vi);
subplot(131); show_slices(imgc);

c_mdl.mk_coarse_fine_mapping.f2c_offset = [0,0,-.3];
c_mdl.mk_coarse_fine_mapping.z_depth = 0.1;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;
imgc0= inv_solve(imdl, vh, vi);

imgc0= inv_solve(imdl, vh, vi);
subplot(132); show_slices(imgc0);

c_mdl.mk_coarse_fine_mapping.f2c_offset = [0,0,.3];
c_mdl.mk_coarse_fine_mapping.z_depth = 0.1;
c2f= mk_coarse_fine_mapping( f_mdl, c_mdl);
imdl.fwd_model.coarse2fine = c2f;

imgc1= inv_solve(imdl, vh, vi);
subplot(133); show_slices(imgc1);

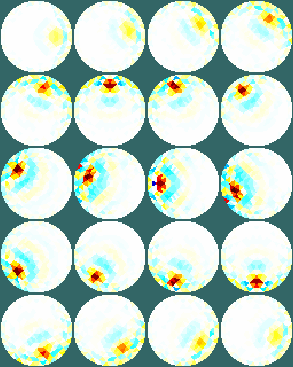
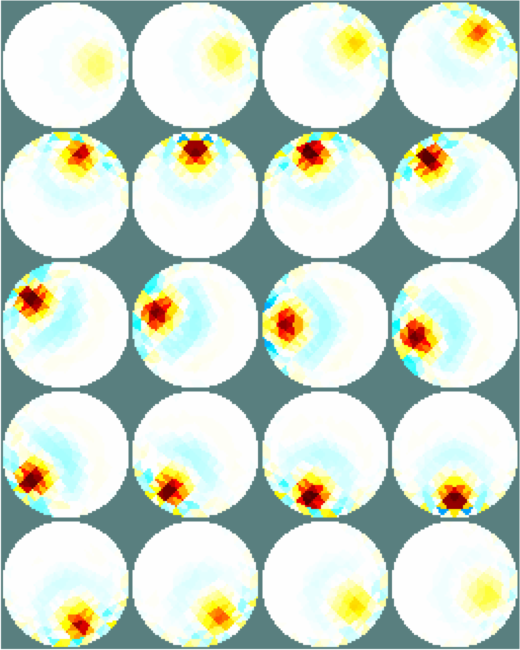
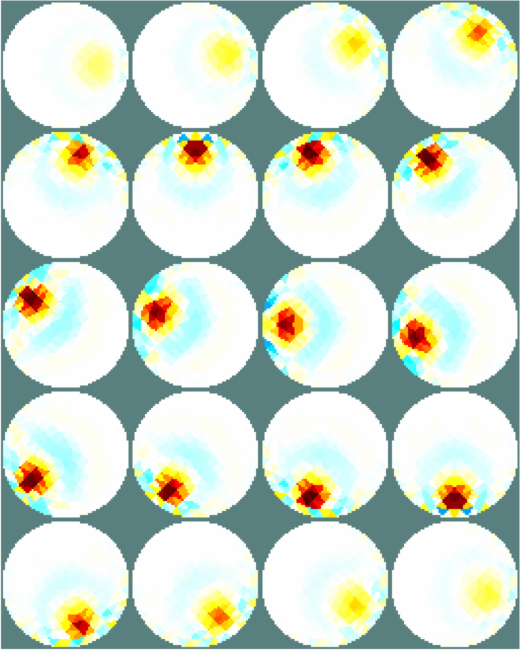
print -r150 -dpng centre_slice06a.png;

Figure: Reconstructed images of a target moving in a helical pattern using difference coarse models Left coarse model with z_depth=∞ Centrecoarse model with z_depth=0.1×scale at upper position Right coarse model with z_depth=0.1×scale at lower positions