EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software

Hosted by

Two and a half dim (2½D) image reconstruction

Thus, the z direction is part of the forward model, but not the inverse. It is thus "half" a dimension.

Fourier Approximation

The 2½D is typically built by constructing a 2D forward model and approximating the effect of the additional z direction through a summation of Fourier transform coefficients. Depending on the formulation, the Fourier summation may represent a finite region on either (for example, a cylinder) or an infinitely large region (for example, a half-space). Course/fine mapping can be applied on top of this to give a fine 2D forward model and a coarse 2D inverse model. The electrodes must all be at the z=0 plane.

For an explanation of the formulation, see the presentation for

Modelling with 2.5D Approximations, Alistair Boyle, Andy Adler, 17th Conference on Electrical Impedance Tomography, Stockholm, Sweden, June 19-23, 2016.

Generally, the formulation used in geophysics uses Point Electrodes Models (PEM). Here we use the Complete Electrode Model (CEM) in the x and y directions, and the PEM in the z direction.

% Models
fmdl = mk_common_model('d2C',16); % fine model
cmdl = mk_common_model('c2C',16); % coarse model
c2f = mk_coarse_fine_mapping(fmdl.fwd_model, cmdl.fwd_model);
imdl = fmdl;
imdl.rec_model = cmdl.fwd_model;
imdl.fwd_model.coarse2fine = c2f;

clf; % figure 1
subplot(121);show_fem(imdl.fwd_model);
title('fine (2d) model'); axis square; axis off;
subplot(122); show_fem(imdl.rec_model);
title('coarse (2d) model'); axis square; axis off;
print_convert two_and_half_d01a.png '-density 75'

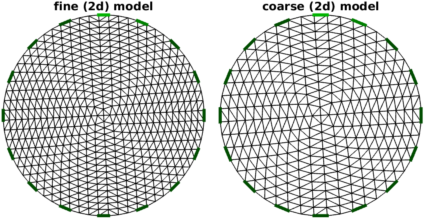
Figure: Left fine (2d) model, Right coarse (2d) model

% test c2f
rimg = mk_image(cmdl,1);
rimg.fwd_model = imdl.fwd_model;
rimg.rec_model = imdl.rec_model;
rimg.elem_data = 1 + ...
   elem_select( rimg.rec_model, '(x-0.3).^2+(y+0.1).^2<0.15^2' ) - ...
   elem_select( rimg.rec_model, '(x+0.4).^2+(y-0.2).^2<0.2^2' )*0.5;
fimg = mk_image(fmdl,1);
fimg.elem_data = 1 + ...
   elem_select( rimg.fwd_model, '(x-0.3).^2+(y+0.1).^2<0.15^2' ) - ...
   elem_select( rimg.fwd_model, '(x+0.4).^2+(y-0.2).^2<0.2^2' )*0.5;
clf; % figure 1
subplot(131); show_fem(mk_image(imdl.rec_model,rimg.elem_data)); axis square; axis off;
title('coarse');
subplot(132); show_fem(mk_image(imdl.fwd_model,c2f*rimg.elem_data)); axis square; axis off;
title('coarse-to-fine');
subplot(133); show_fem(fimg); axis square; axis off; title('fwd fine');
print_convert two_and_half_d02a.png '-density 75';

% Simulate data - homogeneous
himg = mk_image(fmdl,1);
vh = fwd_solve_2p5d_1st_order(himg);
% Simulate data - inhomogeneous
vi = fwd_solve_2p5d_1st_order(fimg);

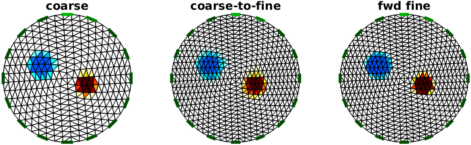
Figure: Left coarse model Centre coarse data mapped to fine model Right fine model

% Solve 2.5D
% Create inverse Model: Classic
imdl.hyperparameter.value = .1;
imdl.reconst_type = 'difference';
imdl.type = 'inv_model';

% Classic and 2.5D (inverse crime) solver
vh.type = 'data';
vi.type = 'data';
img2 = inv_solve(imdl, vh, vi);
imdl.fwd_model.jacobian = @jacobian_adjoint_2p5d_1st_order;
img25 = inv_solve(imdl, vh, vi);

clf;
subplot(131); show_fem(fimg); title('model'); axis off; axis square;
subplot(132); show_fem(img2); title('2D'); axis off; axis square;
subplot(133); show_fem(img25);title('2.5D'); axis off; axis square;
print_convert two_and_half_d03a.png

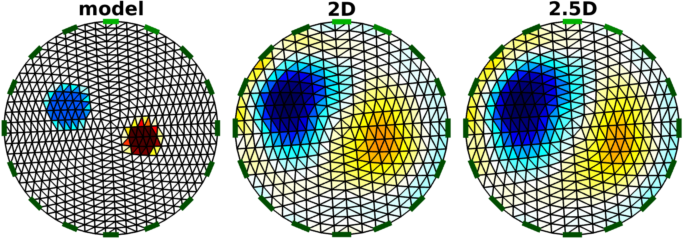
Figure: Left original model Centre 2d reconstruction Right 2½ reconstruction onto coarse model

2D + 3D = 2.5D

The 2½D can also be built as an application of coarse/fine mapping, where the fine (high density) 3D forward model is used with a coarse (low density) 2D inverse model. The 2D model is projected through the 3D model giving constant conductivity along the axis of the projection.

% Build 2D and 3D model $Id: two_and_half_d04.m 5392 2017-04-12 05:22:03Z alistair_boyle $

demo_img = mk_common_model('n3r2',[16,2]);

% Create 2D FEM of all NODES with z=0
f_mdl = demo_img.fwd_model;
n2d = f_mdl.nodes( (f_mdl.nodes(:,3) == 0), 1:2);
e2d = delaunayn(n2d);
c_mdl = eidors_obj('fwd_model','2d','elems',e2d,'nodes',n2d);

subplot(121);
show_fem(f_mdl); title('fine (3d) model');

subplot(122);
show_fem(c_mdl); title('coarse (2d) model');
axis square

print_convert two_and_half_d04a.png '-density 75'

% Simulate data - inhomogeneous
img = mk_image(demo_img,1);
vi= fwd_solve(img);

% Simulate data - homogeneous
load( 'datacom.mat' ,'A','B')
img.elem_data(A)= 1.15;
img.elem_data(B)= 0.80;
vh= fwd_solve(img);

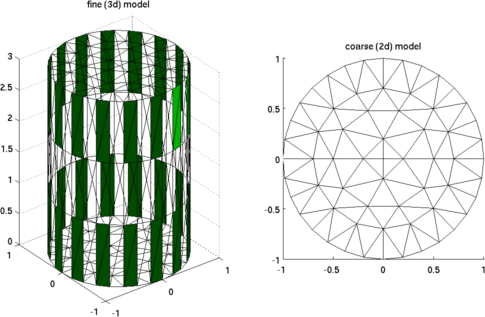
Figure: Left fine (3d) model, Right coarse (2d) model

% Solve 2D and 3D model $Id: two_and_half_d05.m 5392 2017-04-12 05:22:03Z alistair_boyle $

% Original target
subplot(141)
show_fem(img); view(-62,28)

% Create inverse Model: Classic
imdl= select_imdl(f_mdl, {'Basic GN dif'});
imdl.hyperparameter.value = .1;

% Classic (inverse crime) solver
img1= inv_solve(imdl, vh, vi);
subplot(142)
show_fem(img1); view(-62,28)

% Solve 2D and 3D model $Id: two_and_half_d06.m 5392 2017-04-12 05:22:03Z alistair_boyle $

c2f= mk_coarse_fine_mapping( f_mdl, c_mdl );

imdl.fwd_model.coarse2fine = c2f;
img2= inv_solve(imdl, vh, vi);
img2.elem_data= c2f*img2.elem_data;
subplot(143)
show_fem(img2); view(-62,28)

% 2.5D reconstruct onto coarse model
subplot(144)
img3= inv_solve(imdl, vh, vi);
img3.fwd_model= c_mdl;
show_fem(img3);
zlim([0,3]); xlim([-1,1]); ylim([-1,1]);
 axis equal; view(-62,28)

print_convert two_and_half_d06a.png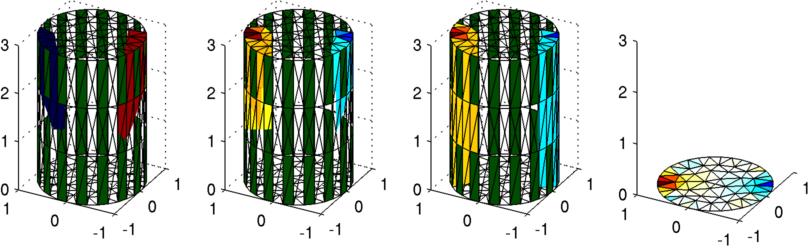

Figure: Left original (3d) model Centre left fine (3d) reconstruction Centre right 2½ reconstruction onto fine model Right 2½ reconstruction onto coarse model