

|
EIDORS: Electrical Impedance Tomography and Diffuse Optical Tomography Reconstruction Software |
|
EIDORS
(mirror) Main Documentation Tutorials − Image Reconst − Data Structures − Applications − FEM Modelling − GREIT − Old tutorials − Workshop Download Contrib Data GREIT Browse Docs Browse SVN News Mailing list (archive) FAQ Developer
|
Simulating Geophysical measurements around a boreholeCreate 3D FEM model of the gallery
% Create 3D model of a tunnel $Id: tunnelsim01.m 6455 2022-12-07 00:37:14Z aadler $
N_elec = 16;
shape_str = ['solid incyl = cylinder (0,0,0; 1,0,0; 1) -maxh=1.0; \n', ...
'solid farcyl = cylinder (0,0,0; 1,0,0; 5) -maxh=5.0; \n' ...
'solid pl1 = plane(-5,0,0;-1,0,0);\n' ...
'solid pl2 = plane(5,0,0; 1,0,0);\n' ...
'solid mainobj= pl1 and pl2 and farcyl and not incyl;\n'];
th= linspace(0,2*pi,N_elec+1)'; th(end)=[];
cth= cos(th); sth=sin(th); zth= zeros(size(th));
elec_pos = [zth, cth, sth, zth cth, sth];
elec_shape=[0.05];
elec_obj = 'incyl';
fmdl = ng_mk_gen_models(shape_str, elec_pos, elec_shape, elec_obj);
subplot(221); show_fem( fmdl );
view(90,0); print_convert tunnelsim01a.png
view( 0,0); print_convert tunnelsim01b.png
crop_model([], inline('x>=0.5','x','y','z'))
crop_model([], inline('x<=-0.5','x','y','z'))
crop_model([], inline('(y.^2+z.^2)>=1.3^2','x','y','z'))
view(-90,50); axis tight; print_convert tunnelsim01c.png
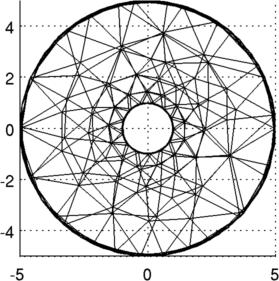
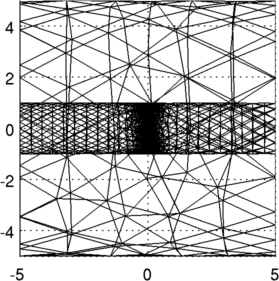
Figure: 3D FEM of gallery from two viewing angles, and a cropped model showing the electrodes Place a simulated contrast
% Create 3D model of a tunnel $Id: tunnelsim02.m 3273 2012-06-30 18:00:35Z aadler $
% Simulation protocol.
stim = mk_stim_patterns(N_elec, 1, [0,4], [0,4], {'no_meas_current'},1);
fmdl.stimulation = stim;
cond_mdl = .1; % in S/m units
img = mk_image( fmdl, cond_mdl);
vs_h = fwd_solve( img);
img.elem_data = cond_mdl*(1 + mk_c2f_circ_mapping(fmdl, [0.25;1.4;0;0.2]) );
vs_i = fwd_solve( img);
show_fem(img); ylim(2*[-1,1]); zlim(2*[-1,1]);
view(90,0 ); print_convert tunnelsim02a.png
view( 0,90); print_convert tunnelsim02b.png
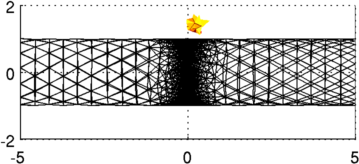
Figure: 3D FEM of gallery and contrast from two viewing angles. Reconstruct images (using full 3D reconstruction)Using the full 3D model, this is an extremely slow reconstruction process; it is also not really recommended since the model size is much too small near the electrodes.
% Create 3D model of a tunnel $Id: tunnelsim03.m 7116 2024-12-29 13:35:10Z aadler $
% Reconstruct entire image (slow)
imdl = mk_common_model('a2c2',N_elec); % placeholder, then change fmdl
imdl.fwd_model = fmdl;
imdl.jacobian_bkgnd.value = cond_mdl;
imgr = inv_solve( imdl, vs_h, vs_i );
imgr.calc_colours.npoints= 128;
slices = [0.0,inf,inf,1,1;
0.5,inf,inf,2,1;
1.0,inf,inf,3,1];
subplot(211); show_slices(imgr,slices);
print_convert tunnelsim03a.png
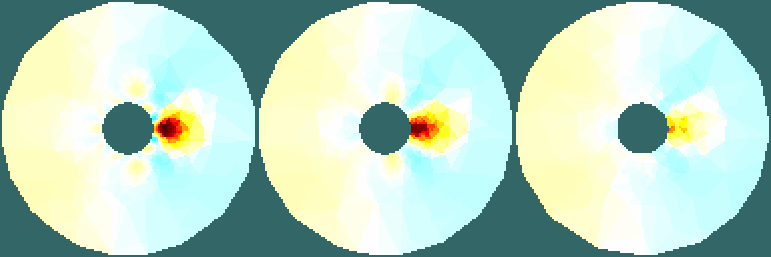
Figure: Slices Reconstructed at x=0.0, x=0.5, and x=1.0. Reconstruct images (on a 2D simple slice)Here we use a slice from a filled 2D circular model. This means that the smoothing prior will be allowed to "fill" through the centre, resulting in image content where we don't expect it to be.
% Create 3D model of a tunnel $Id: tunnelsim04.m 4839 2015-03-30 07:44:50Z aadler $
% Reconstruct to a slice via coarse2fine
% Use a simple circular model without hole.
% Note that this will give the wrong electrode posns
imdl = mk_common_model('d2c2',N_elec);
imdl.rec_model = imdl.fwd_model;
imdl.rec_model.nodes = imdl.rec_model.nodes*5; % Enlarge
imdl.fwd_model = fmdl;
imdl.jacobian_bkgnd.value = cond_mdl;
% Do coarse2fine mapping. Rotate mdl to z dirn
f1mdl = fmdl; f1mdl.nodes = f1mdl.nodes(:,[2,3,1]);
f1mdl.mk_coarse_fine_mapping.z_depth = 1;
c2f= mk_coarse_fine_mapping( f1mdl, imdl.rec_model);
imdl.fwd_model.coarse2fine = c2f;
imdl.hyperparameter.value = 0.3;
imgr = inv_solve( imdl, vs_h, vs_i );
imgr.calc_colours.npoints= 128; subplot(221);
show_slices(imgr); print_convert tunnelsim04a.png
show_fem(imgr); print_convert tunnelsim04b.png
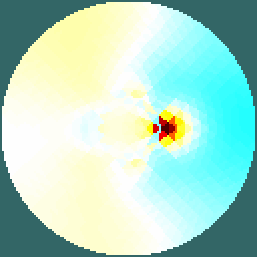 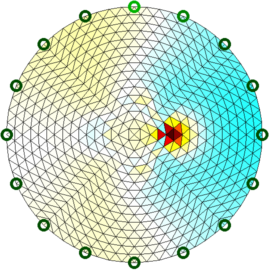
Figure: Slices 2D slices shown in two configurations Reconstruct images (on a 2D conforming geometry)Here we use a slice created to conform to the specified geometry.
% Create 2D model of a tunnel $Id: tunnelsim05.m 2361 2010-11-08 10:50:48Z aadler $
extra={'ball', 'solid ball = sphere(0,0,0;1) -maxh=0.25;'};
cmdl= ng_mk_cyl_models([0,15,3],[0],[0.1,0,0.05],extra);
show_fem(cmdl); print_convert tunnelsim05a.png
show_fem(cmdl); axis(2*[-1,1,-1,1]); print_convert tunnelsim05b.png
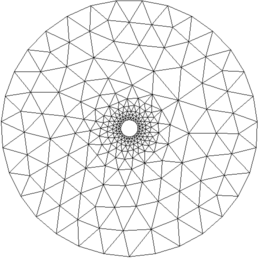 
Figure: 2D FEM model for reconstruction and zoom
% Create 3D model of a tunnel $Id: tunnelsim06.m 4839 2015-03-30 07:44:50Z aadler $
imdl = select_imdl( fmdl, {'Basic GN dif'});
imdl.rec_model = cmdl;
imdl.jacobian_bkgnd.value = cond_mdl;
% Do coarse2fine mapping. Rotate mdl to z dirn
f1mdl = fmdl; f1mdl.nodes = f1mdl.nodes(:,[2,3,1]);
f1mdl.mk_coarse_fine_mapping.z_depth = 1;
c2f= mk_coarse_fine_mapping( f1mdl, cmdl);
imdl.fwd_model.coarse2fine = c2f;
imdl.hyperparameter.value = 0.3;
imgr = inv_solve( imdl, vs_h, vs_i );
imgr.calc_colours.npoints= 128; subplot(221);
show_slices(imgr); print_convert tunnelsim06a.png
show_fem(imgr); print_convert tunnelsim06b.png
show_fem(imgr); axis(3*[-1,1,-1,1]); print_convert tunnelsim06c.png
 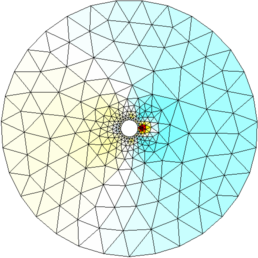 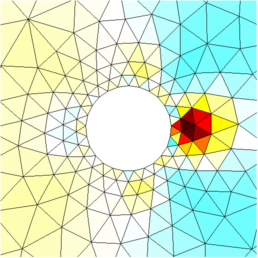
Figure: Reconstructed images |
Last Modified: $Date: 2017-02-28 13:12:08 -0500 (Tue, 28 Feb 2017) $ by $Author: aadler $